In this post I will explore binarized neural networks (BNNs) and recent publications related to BNNs in FPGA 2017. BNNs are popularized by Courbariaux et al. in this paper . The essence of BNNs is that we constrain the majority of weights and activation values in a deep neural network with binary values, either +1 or -1. This allows us to replace expensive arithmetic floating-point operations (multiplication and addition) with highly efficient binary variants: XNOR (negated exclusive OR) and popcount (counting the number of non-zero values). Such architecture is highly rewarding when implemented onto FPGAs than GPUs and CPUs: each of such operations can be easily implemented using tiny amount of LUTs in FPGAs, and the significantly reduced size of weight parameters further gets rid of the off-chip RAMs and the associated von Neumann bottleneck . This advantage makes FPGAs shine in terms of power, speed and potentially cost, differentiating themselves from other computing machines such as CPUs and GPUs for implementing BNNs.

An immediate difficulty that follows binary weight and activation constraints is that the gradient of the loss function cannot be back-propagated in the network. As the activation function \( f(x) \) binarizes values from pre-activation, which casts continuous inputs into quantized results, this function is not continuous:

$$f(x) = Sign(x) = \left\{ \begin{aligned} & +1 & & \text{if } x \geq 0, \\ & -1 & & \text{otherwise}. \end{aligned} \right.$$

We can see that this function doesn’t have a gradient value when $x = 0$, and remains constant $0$ at other positions. Without meaningful gradients, it becomes impossible to train this network, as stochastic gradient descent does not have a gradient to descend. For this problem Bengio et al. suggest that we could instead propagate the gradient “straight-through”. In other words, it means that we ignore the gradient contribution of the non-linear activation function, effectively treating the activation function as an identity function with a constant gradient of $1$, this way the back-propagated gradient remains continuous. BNNs from Courbariaux et al. employ saturation in addition, such that if the parameter $r$ to be adjusted by its gradient $g_r$ is outside the range of $[-1, 1]$, we cancel its gradient by setting the gradient to $0$, to ensure $r$ saturates at $\pm 1$.

XNOR-Net from Rastegari et al. proposes an almost identical network structure, with slight differences in the ways they binarize weights and activations. Instead of using the straight-through gradient estimator we have discuss above, they directly quantize weights and activations, and introduce scaling factors of binary computations to closely approximate real-valued computations.

FPGA 2017 BNN papers

The paper “Accelerating Binarized Convolutional Neural Networks with Software-Programmable FPGAs” that I am going to review is from Ritchie Zhao et al., which proposes a new accelerator architecture for BNNs on a Zynq 7Z020 FPGA. The illustration of the architecture, from their paper, is shown in the figure below.

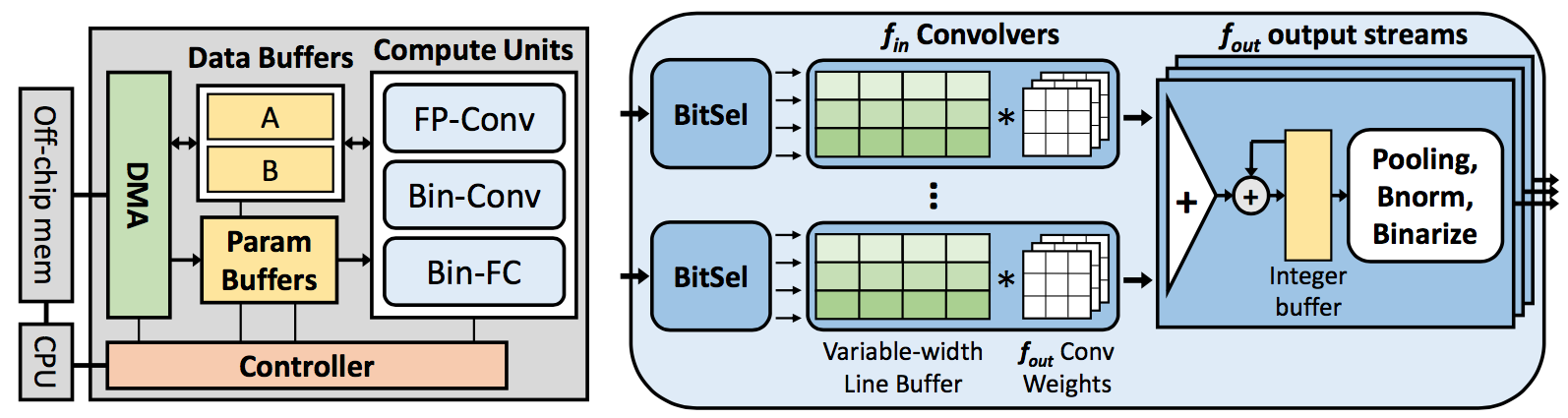
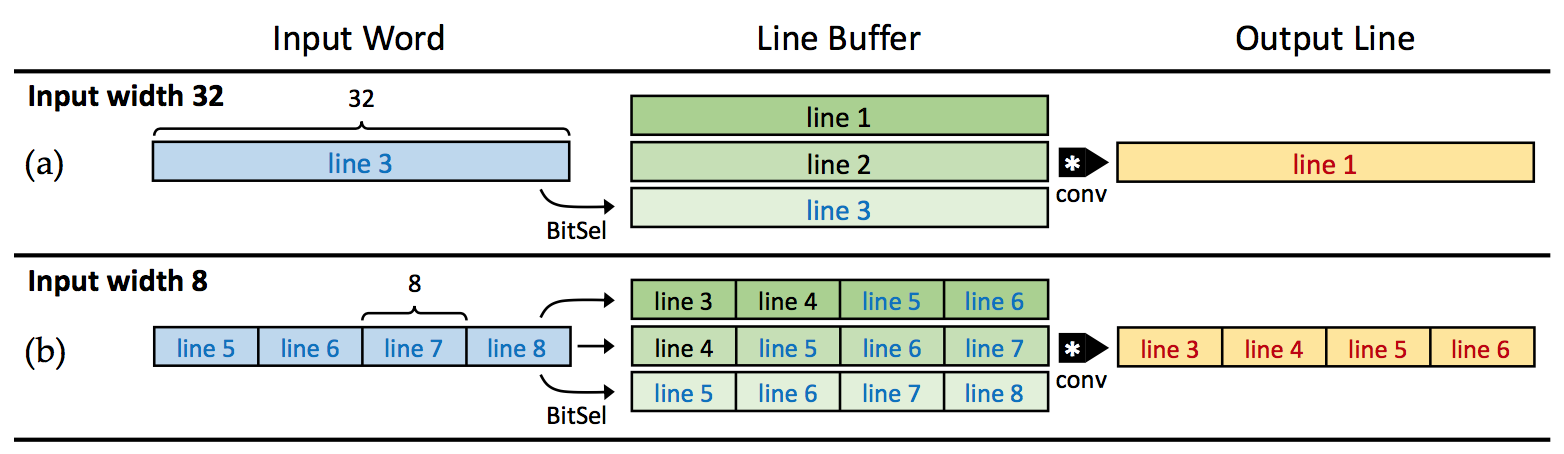
The diagram on the left shows the high-level control- and data-flow hierarchy, the one on the right shows the internal components of the Bin-Conv unit. The authors recognized that because BNNs use 1-bit inputs in convolution, line buffers in convolution must be designed with consideration of a wide-range of image widths. The authors therefore proposes the line buffers to have variable widths, and adapt to different configurations for various input widths, as shown in the figure below they produced in the publication. This allows them to maintain high throughput for distinct sizing of convolution layers.

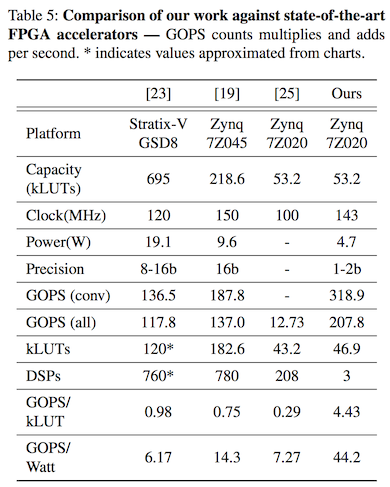
So what is the main takeaway from this? From the comparison results (figure below) against other RTL- and OpenCL-based FPGA implementations, I think personally it signals the viability of [high-level synthesis (HLS)][hls] in the context of linear algebra applications. Although HLS does not give you the same extent of design flexibility when compared to RTL, the low design costs associated with HLS could still vastly outweigh the disadvantage of a slightly lower performance.

The next paper “FINN: A Framework for Fast, Scalable Binarized Neural Network Inference” from Umuroglu et al. presents a similar approach to implement binarized architecture on FPGAs.

Their FPGA implementation remaps convolution into matrix-multiplication, and further interleaves multiple image channels to be processed by interleaving filters to increase parallelism. This is illustrated below.

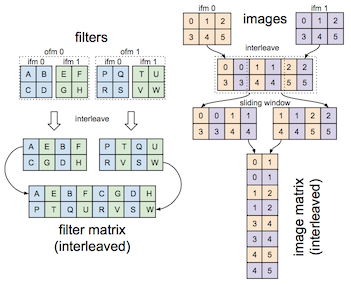
With the recent trend of realizing deep neural networks using high-level synthesis, the authors follow suit by using Vivado HLS in their work and produce results that rival prior work in RTL implementations.

My thoughts

The current accuracy of deep neural networks is largely enabled by a vast number of parameters introducing redundancy. Optimization of these networks by reducing this redundancy, also known as network compression, is the key to future breakthroughs in running them efficiently in all computing devices. Such techniques include pruning and quantizing network parameters via deep compression , training neural networks at a low precision and others.

BNNs, owing to their minimal weight representation ($\pm 1$), also achieve network compression via low precision, although much more extreme than other approaches. I believe for this reason, their applicability has thus been limited to networks that are already redundant in the number of parameters, so that the capacity (ability to learn) of the algorithm greatly exceeds the complexity (difficulty to learn) of the problem at hand, such as AlexNet on ImageNet classification, MNIST, CIFAR-10 and SVHN.

DoReFa-Net seeks to generalize the extreme bitwidth compression in BNNs by extending the formulation to multi-bit weights and activations. The authors show that for networks with sufficient capacity, we can get away with binary weights and 4-bit activation, their minimal ResNet-18 with such configurations manages a 59.2% top-1 accuracy.

The problem here, I believe, lies within the tug war between performance and network capacity. A sweet spot necessitates achieving the optimal performance given a required capacity constraint. This problem is unfortunately very difficult to answer, as we don’t have a way to understand network capacity in a well-defined form for now. If we’re in a competition to optimize DNNs with no experiences to help us, luck would eventually becomes irrelevant in the long run (regression to the mean ), only the most productive ones at trial-and-error would prevail. So from now I should procrastinate less and work more.